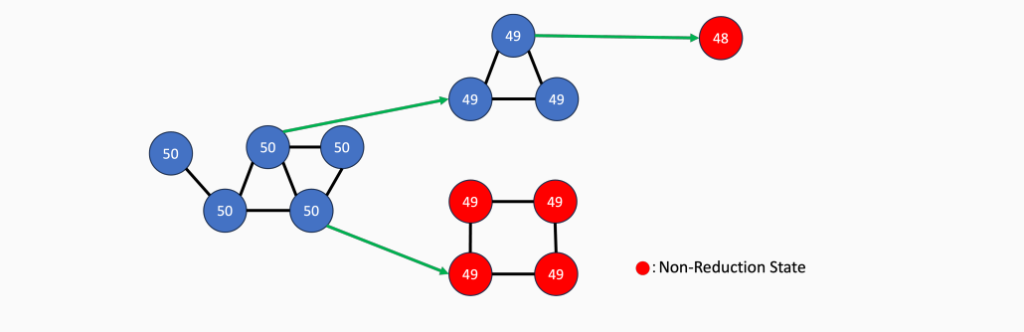
行き詰まったら、一度戻って考え直します
荒井くんと市川くんの行列積の掛け算最小記録論文がThe International Symposium on Symbolic and Algebraic Computation (ISSAC) に採択されて、荒井くんが口頭発表をしてきました。1988年から毎年開催されている由緒正しい研究会です。
Yamato Arai, Yuma Ichikawa, and Koji Hukushima
“Adaptive Flip Graph Algorithm for Matrix Multiplication,”
ISSAC ’24: Proceedings of the 2024 International Symposium on Symbolic and Algebraic Computation, July 2024, Pages 292 – 298
統計物理学の研究室としては主戦場ではないこともあり、ISSACはよく知らない会議ですが、土台となったFlip graph論文が2023年のこの会議で発表されていたので、投稿してみたわけです。採択されてよかったです。
arxivにプレプリントをあげてから、半年が経って、遠い昔の話のようになってきました。
当時のやや熱めの研究解説はこちらにあります。:行列積問題の記録更新論文
会議への投稿に際して、plus transitionによるグラフの連結性の証明も加えています。この話をいろんなところですると、反応が人によって大きく違うんですよね。パズルを解くような面白さなので、深い面白さは有るのか無いのかよくわからないのですが、この面白さをわからないのだと、うちには合わない気がします。
行列の掛け算の計算量がN^3より小さくなるなんて思いもよらない?のですが、Strassenの話は Nature of Computationに書いてあるんですね。このことを教えてくれたのは高橋惇くんです。この本はなんでも書いてあるんです。。。Strassenの話しなんか普通知らないと思うし、自分も数年前には知らなかった。でも、Krauthさんは知ってたんですよね。この前、行列積の話をしたら、「えーと、それはなんだっけ、あのー」って感じで名前はでてこなかったけど存在は知ってて流石です。
2×2の2つの行列の積に必要な行列要素の積は素朴には8回必要ですが、7回でよいことを示したのが、Strassenの話です。そんな一つ減ったくらいでなんなんだ。そもそも物理とか関係ないじゃないか?って、そのとおりですよ。ブロック行列に適用すると、行列積の演算は3乗ではなくて、2.8乗くらいでできることになりますが、実際に使ってみてもそんなに速くはならないです。通常の行列積は行列要素を連続参照できるので、メモリー周りとかいろんな計算機の性質が見えちゃって速くならない。理論的にはその指数は2.3乗くらいまでいけることが示されています。ただ、それも具体的なアルゴリズムの構成方法は示されていなくて、素朴な計算では前の係数がめちゃくちゃ大きいことになっています。超楽観主義的には掛け算の演算も足し算の演算くらいまでは下げられるかもという説もあります。。。。つづく。
(2025.2.14)
何をつづきで書こうとしていたのかもはや思い出せないのですが、ちょっと個人的に激アツニュースが飛び込んできました。なんと、荒井くんの見つけた5×5の行列積の94手数が抜かれました!
[Submitted on 6 Feb 2025]
Flip Graphs with Symmetry and New Matrix Multiplication Schemes arXiv:2502.04514
Jakob Moosbauer, Michael Poole
記録は抜かれるものです。もう更新されないなぁと思っていたのですけど、あるものなんですね。素晴らしい!
(2025.4.8)
この論文を荒井くんが解説してくれました。なかなかにすごいです。行列積分解についての経験的な対称性について考察して、対称性で区切られた部分空間の探索をすることで記録を更新しています。一般に、対称性を課した探索は面倒になるのですが、この提案方法はそうではないようです。ただ、部分空間の中に解がある保証はないので、初期条件で探索するしかないのですが、そこはちょっとむずかしそうです。いくつか驚きポイントがあるのですが、そのひとつはStrassenの2×2の最適解もその対称性を持っていて、天才でなくても見つける手順を具体的に示していることです。対称性は素朴なのですが、行列積分解がその対称性を持つ必要はないし、それ以外にもっとよい分解もあるかもしれない。それでもStrassenは持っていたんです。もっと深いものがあるかもしれません。