薄膜ラウエ振動のベイズ統計的解析

崎下くんの論文がJournal of Physica Society of Japanに掲載されました。
Bayesian Estimation of Thin-film X-ray Laue Oscillation Using Markov Chain Monte Carlo Method
Yuki Sakishita, Fuyuki Nabeshima, Atsutaka Maeda, Koji Hukushima
Journal of the Physical Society of Japan, 94, 014001 (2025)
10.7566/JPSJ.94.014001

ちょっと久しぶりですが、この論文とその背景を解説します。

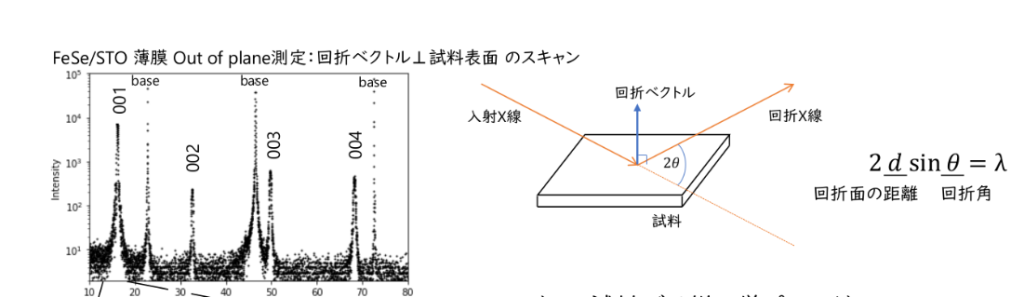
この論文では、2024年3月に卒業した崎下くんが修士課程のときに実験で得ていたFeSe薄膜のX線ラウエ振動をベイズ統計で解析し、膜厚を推定しました。この研究では得られた実験データから統計モデルをモデリングし、その解析から知りたい物理量を推定するという極めて地に足がついた、どんな実験データでも同じようにでき、それでいてやってみるといろいろ悩むなぁーという解析を実データをもとにやってみた研究です。個人的にはとても面白いと思っています。最近のデータ科学では、「深層学習を使って精度が〇〇倍になった」とか、「ベイズ先端計測で見えないものが見えるようになった！」とかそういうのが流行る時代なのですが、

データから学習するのではなくて、データにしゃべってもらう感じ

がよいと思うのです。

この論文で解析したX線回折では、X線を薄膜試料に入射したときのラウエ回折の式はわかっています。この計測の物理プロセスは既知であり、それを統計モデルに組み入れた単純な回帰で十分な状況と考えられるかもしれません。ただ、考えてみますと、X線を試料に照射して回折X線を計測する…だけで計測データが得られるわけではなく、計測装置の計測過程も物理プロセスで表されるのですが、そこはうまくモデル化できるかというとそんなに簡単ではありません。例えば、計測装置に入るX線の入射角は有限の幅を持っていますし、それをどのように統計モデルに反映するかは自明ではありません。そして、計測過程には計測ノイズが入ります。X線の実験は計数計測ですので、素朴にポアソン分布に従うと思いますが、実際のデータはそれを示すかどうかを詳しく調べました。

何も考えないで最小二乗法を使うことはノイズモデルにガウス分布を仮定しているとみなせるのはベイズ統計の教えてくれるところです。現場的にはX線のカウント数はケタで異なるので、そのまま最小二乗法でフィットしてしまうと、カウントの大きいところに「引っ張られる」感じがするので、対数をとってから回帰してみたくなります。それは対数にガウス分布ノイズがのっていることを仮定することに対応します。これらは計測過程を考えると素朴には正当化されない気がしますが、それらのモデルにポアソン分布モデルは勝てるかということは一つの関心事です。それにもう一つ、X線回折解析でよく使われている修正ガウス分布と呼ばれるポアソンをちょっと変更したモデルも対象にしました。どれがよいかはベイズ統計ではエビデンスで判断しようという作戦です。いまではエビデンスはMCMCで計算できます。結果は修正ガウス分布が勝ちました。ポアソン分布もかなり良い感じですが、ガウス分布や対数ガウス分布はダメでした。ある意味で予想通りですが、それがちゃんと出てきたのは気持ちが良いです。予測分布も描いてみたので、それをみると、なるほどねって感じです。これは…

べき則の指数をフィッティングするときって、両対数取ってから回帰すると線形回帰になるから、普通に…少なくともずっとこれまでやってきたのですが、それは間違ってるかもってことと同じなんですよね。

だけど、修正ガウスモデルが勝つのはなぜかというのはなぞです。原理的にはポアソン分布なはずだと思うのに、エビデンス的には勝てない。偉大なる経験則が勝つのはなぜかは面白い問題だと思います。我々は答えをもっていないのですが、どこかの講演で話したときに熊本大学の赤井先生に「入射角が混ざっててポアソン分布を重ねてしまった結果を計測しているからでは」と指摘されて、その可能性は大きいと思います。勉強になります。

ここまで計測に関するモデリングの考察でしたが、薄膜のモデリングも必要で、そもそも均一な膜など実験的にはできないと思うので、膜厚が空間的に揺れているモデリングも試しています。具体的には異なる膜厚が分布していて膜厚の値ごとに異なる強度の混合分布を推定してます。

このあたりは考えると奥が深くて、データ解析する立場からは、用いている統計モデルが真のモデルを含んでいる保証はないと思うものなので、均一膜厚のモデルで解析したらこうなるし、複数膜厚モデルで解析したらこうなると考えるですが、物理の立場からは「真実はいつもひとつ」と思っているので、真のモデルは一つだし、そうでないモデルで解析するなどありえないと思うものなんですよね。たとえば、計測のモデルはちゃんと解析に含まれているかというとそうではないわけで、認識を変える必要があるかと思います。ただ、難しいことはできないので、できる範囲でできることから考察することが大事であって、それをふっとばして、見えないものが見えることはないと思っています。