馬蹄型事前分布によるスパース推定の
統計力学的研究
2023年3月に卒業した長野くんの研究が論文として出版されました。次の二つの研究論文が発表されました。
- Phase transition in compressed sensing with horseshoe prior
Yasushi Nagano and Koji Hukushima,
Phys. Rev. E 107, 034126 – Published 17 March 2023 - Effect of global shrinkage parameter of horseshoe prior in compressed sensing
Yasushi Nagano and Koji Hukushima,
J. Stat. Mech. (2024) 053402
すぐに出版されると思ったのですが、そうはいかず、この解説もなかなか公開できませんでした。我々の問題ではなかったので、ちょっともやもやしますが…
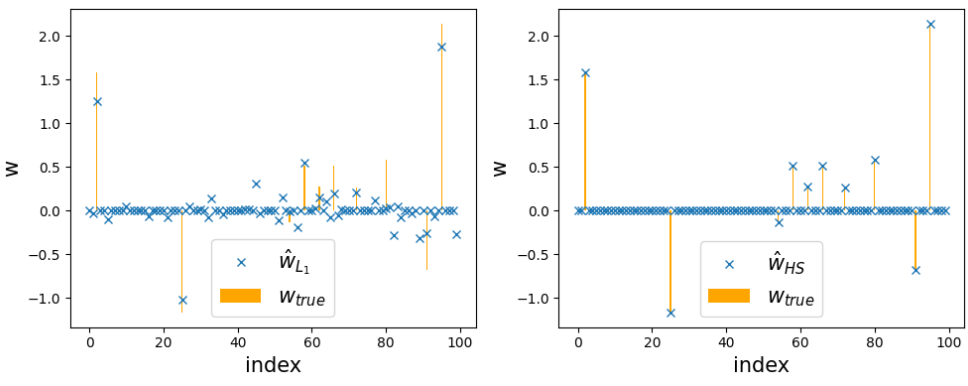
さて、長野くんの研究はスパース推定と呼ばれる推定問題に対する馬蹄型事前分布の方法という、ちょっといかつい名前の方法の性質を統計力学的に研究した最初の論文です。高次元ベクトルのスパース性に注目したスパースモデリングには様々な展開があり、その中で推定にフォーカスした技法にスパース推定や圧縮センシングがあります。これまで広く知られている方法はL1正則化の方法で、推定ベクトルの要素を効果的に刈り込む、すなわちゼロにすることができます。LASSOなどは聞いたことがあるかもしれません。様々な応用の中で、L1正則化の方法は効率良いアルゴリズムも提案されて発展する一方で、バイアスの影響(真の要素を小さめに推定)や擬陽性の問題(真の要素はゼロなのに有限と推定)が顕在化してきました(上の図の左側)。スパース推定の目的にも依りますが、場合によってこれは深刻な問題になります。
その対策は当然議論されていて、一つの方向性に推定するパラメータの事前分布の分散を混合することがあげられます。ベイズ推定の形式では事前分布にもう一つ階層構造を入れて混合を取り入れますが、特別な混合分布に対して事前分布を形式的に表したときに馬蹄型になるモデリングがこの馬蹄型事前分布の方法です。長野くんはこの問題を統計力学的に定式化して、真の信号からノイズなしの線形観測をしたデータを入力として真の信号を復元する条件をクリアに導出しました。この馬蹄型事前分布の方法には分散混合の際に、localとglobalと呼ばれる性質の異なる二つのパラメータがあって、その役割をそれぞれ解析をしたのが上の二つの論文になります。
最初の論文では、localパラメータの役割に注目して、真の信号復元限界を統計力学を用いて明らかにしました。どうして統計力学なのかはいろんな説明の仕方があります。復元しようとする信号を力学変数として確率分布をカノニカル分布の形式に表すと、ノイズのない状況は絶対零度の統計力学に対応することができます。そのときに真の信号から観測されるデータが復元信号間の相互作用を与えます。これはベイズ推定の問題に共通の性質ですが、真の信号を確率的に生成する設定では、相互作用が確率的に決まるランダム系のスピン系と考えることができます。となると、レプリカ法などランダム系の統計力学の技法を用いて解析が…場合によっては可能になります。これは、いわゆる情報統計力学の王道的な設定かなと思います。
ちなみに私は情報統計力学は苦手…自然科学ではないので、どのように注目すべき現象を見出してくるのかってところが腕の見せどころなのですが、それが見きれなくてオモシロポイントがピンと来ないんです。ただ、上述のスパース推定の問題点に対して、この馬蹄型事前分布の方法でどのように改善されるかは一つの論点になります。これはちょっと面白い…ということを長野くんに教えてもらいました。長野くんは、復元限界がL1正則化から少し改良されて、擬陽性の割合も有意に小さいことを理論的に示しました。なかなか面白い研究だと思っています。
二本目の論文はglobalパラメータに注目して、解析を進めています。このパラメータをチューニングすれば復元限界はさらに改良される気はします。実際に、パラメータを変化させると、theresholding関数と呼ばれる縮小写像を表す関数が、ある意味で理想的なL0正則化のものに近づいていきます。一方で、L0正則化の推定方法はNP困難の意味で解けないので、globalパラメータを変化させ過ぎると実質的に解けない推定方法に帰着されてしまうことも想像できるわけです。その様子を丁寧に調べ上げました。ここでも統計力学の手法を用いましたが、レプリカ対称性の仮定の正しいところでは、その鞍点条件が求解方法の一つである近似的メッセージ伝搬法(Approximate Message Propagation; AMP)の時間発展と形式的に一致するために、アルゴリズムの挙動にも言及できるところが大きいです。その解析を通じて、求解達成条件を議論することが可能になります。この求解達成条件を考慮してglobalパラメータを最適制御すると、復元限界は第一論文の限界線からさらに改良されています。また、「自由エネルギー地形」をみることである種のダイナミクスが議論できることは統計力学の視点でのめっちゃくちゃ面白いところです…と思っているのですが、これを具現化する例はそんなにあるわけではないと思ってて、ここが長野くんの研究の注目点です。
というわけで、こういうことが情報統計力学の面白いところなのか?というのがやっとこのタイミングでわかってきた感じです。一周遅れています>自分。物理側から見て、機械学習とか情報理論の問題を眺めるということは、顕在化された現象の理論的な説明がこういう風にできるところであろうと思います。機械学習の問題を物理の言葉で説明するってのとは全然違う。あくまでも命題は機械学習側にあって、数学的に証明するのではなくて(物理は証明は苦手)、典型解を物理学の視点なり技法で求めちゃうということです。昨今の機械学習ブームが来て、現状は深層学習などの機械学習の技術を使って、物理学のかゆいところを攻めるというのが主流かと思います。まあ、それも思想は違うし、それはそれでやっててねって感じです。
それで、長野くんのこともちょっと触れておきたいです。けど、それは本人にお話してるからいいか。
彼はこの研究室に来たときには、オセロ世界4位だったのですが、卒業して、ちょっと本気出したみたいで、2023年世界大会で優勝しちゃいました。世界1位になったのです。この人、オセロも強いのですが、レプリカ計算できる人なんです。