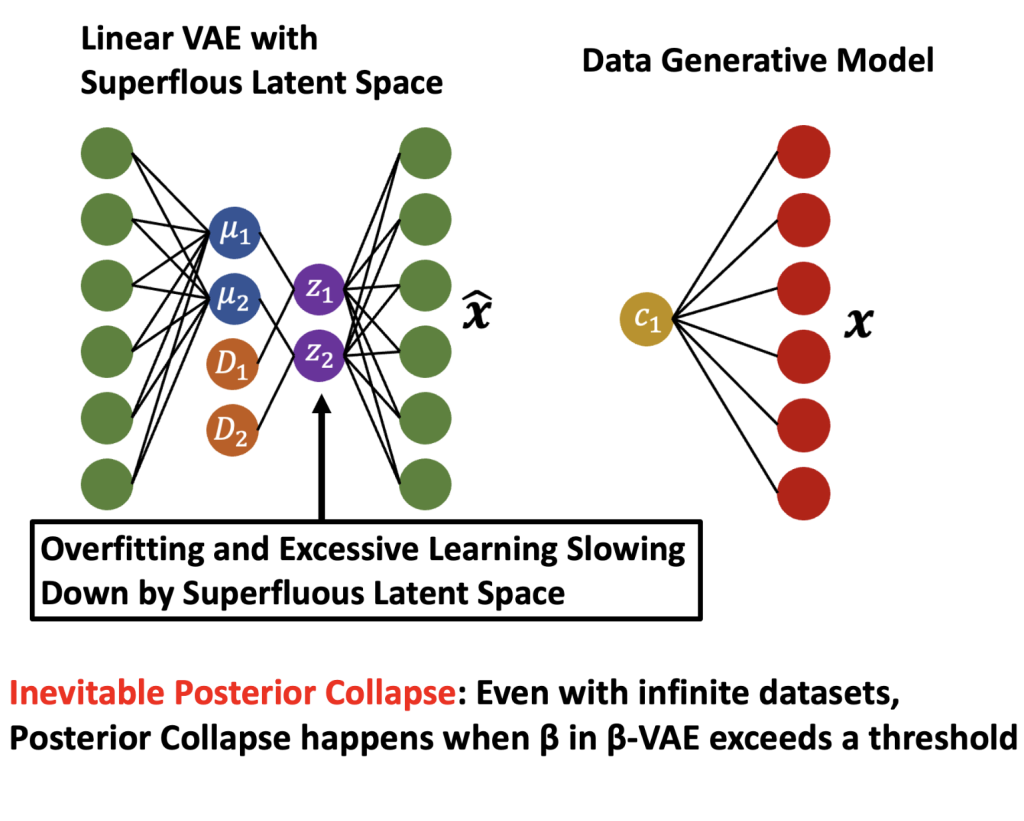
Learning Dynamics in Linear VAE:
Posterior Collapse Threshold, Superfluous Latent Space Pitfalls, and Speedup with KL Annealing

市川くんの研究が、The 27th International Conference on Artificial Intelligence and Statistics (AISTATS)に採択され、５月２日から４日に開催の会議で発表してきました,。当研究室としては、機械学習などのトップカンファレンスには縁がなかったわけです（物理の分野にはカンファレス文化はないのでね）が、市川くんが積極的に応募して、採択が叶いました。論文はこちらからも見られます。
Learning Dynamics in Linear VAE: Posterior Collapse Threshold, Superfluous Latent Space Pitfalls, and Speedup with KL Annealing
Yuma Ichikawa and Koji Hukushima
ArXiv版はここから：arXiv:2310.15440

周辺の解説をします。この研究ではVariational AutoEncoder(VAE)と呼ばれる潜在空間を利用する生成モデルの一つです。VAEは深層学習としても使われる潜在空間モデル、画像や文章や音楽などの生成モデルとして多くの応用がされています。ネットにもいろいろと解説は出ているみたいです。この研究ではそのVAEの学習ダイナミクスについて詳しく調べています。めちゃくちゃ大雑把にいってしまうとVAEはエンコーダーで潜在空間に飛ばしてデコーダーで生成するネットワークをデータから学習します。その際に、たびたび潜在空間での事前分布とエンコーダーの近さを罰金項として損失関数として学習します。この罰金項が大きいと、事前分布に引っ張られ過ぎてposterior collapseと呼ばれるよくない状況が出てきます。うまく罰金項を調整して、このposterior collapseは避ける工夫は常に求められています。この研究では現実に使われるものよりも簡単な設定であるLinear VAEを考え、学習のダイナミクスの統計力学的解析を行いました。

学習するパラメータはエンコーダーとデコーダーのネットワークの重みです。ここでは、通常行われるようにデータから確率勾配法（Stochastic Gradient Descent; SGD) で損失関数を減少させる方法で学習します。確率的にデータを参照するために、その学習過程は確率的なダイナミクスになります。その確率過程では学習するパラメターである重みをつぶさにみることではなく、時々刻々変化する汎化誤差の様子に興味があります。その状況は、気体分子の個々の運動に興味があるのではなくて、圧力や温度などマクロな変数の挙動を知りたいことと…似ています。そこで、ミクロなSGDの時間発展則から、着目するマクロな秩序変数のダイナミクスを導出します。ここで「着目する」は、「汎化誤差を記述するに十分な」を意味します。市川くんの研究では、このマクロ変数のダイナミクスが決定論的な常微分方程式に集中することを数学的に示しました。

そして、そのマクロ変数のダイナミクスを使って、汎化誤差のダイナミクスが書き下せたところがポイントです。先の罰金項の係数を適当に決めて、微分方程式を解いてみると、汎化誤差に長時間に渡って定数になるプラトー現象が見られます。そのまま係数を大きくすると、プラトーはどんどん長くなって、最終的にはプラトーのまま無限大時間まで続くことが示されました。つまり、罰金項の係数があるしきい値よりも大きいと汎化誤差はどんなに長時間学習しても減らず、posterior collapseから抜け出すことはできないということです。しかも、この現象はデータ数を増やしても解決しないことも示されました。これは、学習到達可能ー不可能のようなある種の動的相転移のように見えます。このことは常微分方程式の固定点の情報でもわかり、その安定性解析から引き込まれる漸近的な時間スケールもわかってしまいます。linear VAEという簡単化した生成モデルで相転移の存在を示唆するのは統計力学的アプローチの大きな特徴と言えるでしょうね。

さらに、学習後の定常状態の汎化誤差を最小にする意味での最適な係数もこの設定の元では決めることができます。まずは有限の値をとることが明らかにできたことが重要で、それは係数のチューニングに意味があることを示唆しています。しかも、この定常状態が学習係数と呼ばれるダイナミクスの基本的な時定数に陽に依存することも面白いし、さらにそのゆっくり極限がレプリカ解析と一致します。これは数理的にはめちゃくちゃ非自明な結果だと思います。ちょっとしびれるんですけど…この他にもいろいろ市川くんが調べていて、応用的には係数をアニーリングしたりするわけですが、適当なアニーリング・スケジュールの元での学習ダイナミクスも調べることができます。こんな結果を表すべく、てんこ盛りにしたのがこの論文のタイトルです。

市川くんの関連するこんな論文もArxivに上がっています。
Dataset Size Dependence of Rate-Distortion Curve and Threshold of Posterior Collapse in Linear VAE
Yuma Ichikawa, Koji Hukushima, ArXiv:2309.07663

以前に平間くんとオンライン学習のダイナミクスを調べて、論文にまとめてました。弱学習器の集団学習でその頃ランダムフォレストとかあったのかなぁ、ブースティングとかでてきた頃だったかな…そして、今でいうところのミスマッチで、学習不能な生徒の設定のパラメータの時間発展を巨視的なパラメータの常微分方程式を導いて、汎化誤差のダイナミクスを調べていました。基本的にはそれと同じことを現代的な確率勾配法の学習ダイナミクスを見ていたのですが、今回はもう少し数学的にちゃんと示せるところが最近の理論的な発展と言えるでしょうね。そんな進展があることを私は知らなかった。市川くんのリサーチ能力の凄さです。その技法は統計物理学の問題でも使えるだろうというのも市川くんのコメントで、確かにスピングラスのダイナミクスとか今なら見えることもあるかもしれません。当時は、定常状態のレプリカ解析とか考えていなかったけど、それもやればできることなのかなぁ。ブースティングのダイナミクスも現代的な視点からみるとよいことはあるだろうかね。