吉山くんのテンソルくりこみ群による
古典フレストレート系の研究
今年の3月に卒業した吉山くんのテンソルネットワークくりこみ群を古典フラストレート系に応用した力作論文がPhysical Review Eに掲載されました。
https://journals.aps.org/pre/abstract/10.1103/PhysRevE.108.054124
https://arxiv.org/abs/2303.07733 ArXiv版からはいろいろ修正されているので、出版論文の方をご覧ください。
この論文ではテンソルくりこみ群の方法を用いて、もっとも単純な古典フラストレート系の一つであるJ1J2イジング模型と呼ばれる統計力学モデルの相転移を調べています。この模型の絶対0度の秩序構造は自明にわかっていますので、自明でないところは有限温度でおこる相転移と言えます。これまでに長い研究で、多くのことはわかってきていて、例えば、この模型のJ2が大きい領域では二次相転移がおきて、その際の臨界指数が相互作用パラメータに陽に依存する独特な普遍性クラスに属することが示唆されたりしています。ただし、相互作用の競合が大きい領域では一次相転移になることが示唆されていて、それは本当に起こるのか?、あるいは二次相転移と一次相転移が切り替わるパラメータはいくつか?という問いには確定的な答えはありませんでした。例えば、別の数値計算手法であるモンテカルロ計算で扱えるサイズに制限があり、そのサイズでは普遍性クラスや1次相転移との境界はクリアにはわかっていませんでした。実際にモンテカルロ計算をしてみると、スピン数が5122くらいのサイズになると、熱平衡状態を作るのは結構しんどいというか、私のコードだと一週間くらいの計算では無理っぽいです。そこで、テンソルくりこみ群の方法で扱える巨大なサイズを調べれば、100002くらいまで調べてみればすぐに答えは導ける…だろうという淡い期待と言うか、練習問題的な感覚は見事に打ち砕かれました。
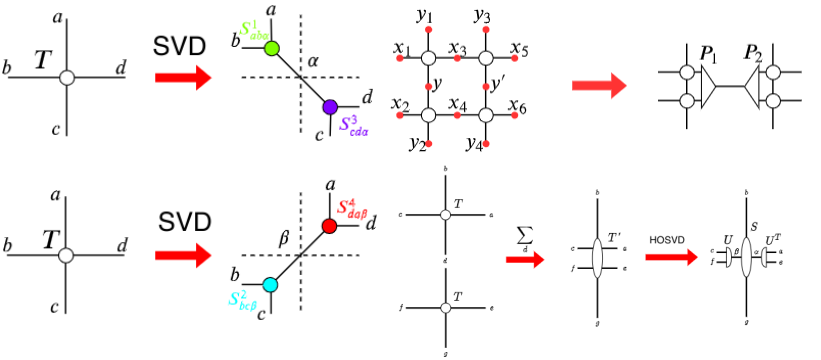
テンソルくりこみ群にはボンド次元とよばれるくりこみ計算の際のテンソルの縮約をとるときのカットオフが数値計算の精度を決めています。ただ、どのようにその精度が決まっているかは全く非自明です。大きくすればよいことは確かですので、ボンド次元を大きくしながら、十分大きいときの物理量の収束を確かめたいわけですが、それがそんなに単純ではない。観測物理量を見ている限りはとても単調に精度があがるようには見えないのです。たとえば、相互作用パラメータの値に依存して、あるボンド次元では1次相転移に見えますが、ボンド次元を増やすと二次相転移に見え、更に増やすと再び1次相転移に見えるようなことが起こります。もうこれでは何が真実かなのかはすぐにはわかりません。この制御のできなさ加減が簡単に心を折ります。テンソルくりこみ群を使っている研究者はこの難儀な性質に耐えているなぁと感心します。
そんな状況で議論を尽くして、数値計算結果をまとめたのがこの論文です。よくあるテンソルくりこみ群のようにくりこみをどんどんやってしまった最後の結果だけをみるのではなくて、途中の有限サイズの結果を追いかけるのは良かったと思います。そのことで、ある種のクロスオーバーを見ることができました。その解釈は必ずしも自明ではないですが、ボンド次元を一定のままくりこみを繰り返すとあるくりこみ回数を超えると数値誤差のために別の固定点に吸い込まれているという一定の解釈を与えることはできます。さらに、臨界指数を評価するDlog plotや数値計算の整合性をチェックするClausius-Clapeyron関係式など、随所に胡椒が振りかけられている論文です。
フラストレーション系でももっとも単純であろうこのJ1J2模型でもこれくらい難しいのだということと、テンソルくりこみ群の難しさが伝わるとよいと思います。このサイズをモンテカルロ法では調べることはできないので、これ以上の手の出し方はわかりません。テンソルくりこみ群にはさまざまな亜種が開発されているので、精度のよい手法を今後も追求すべきと思います。少なくとも調べられるサイズは他の方法を圧倒しているので、希望の星ではあります。ゆくゆくは3次元スピングラス問題につながるとよいと考えています。
さて、テンソルくりこみ群を福島研で研究したのは吉山くんがはじめてで、ノウハウから何からすべてを彼一人でやりとげました。私はなんの知識も持っていなかったので、ほぼ何も指導できない。Kadanoffの最後の?レビュー論文に惹かれて彼にパスを出しただけでした。テンソルネットワーク計算のプロなら、もっと賢く展開できたかもしれないですが、この結果は誰が計算しても変わらないのですから、むしろこの結果を論文に仕上げたのは我々だからではないかとも思います。いや、吉山くんだからです。