Deep Boltzmann Machineの統計力学的研究

市川佑馬くんのDeep Boltzmann Machineの論文が掲載されました。
Statistical-mechanical Study of Deep Boltzmann Machine Given Weight Parameters after Training by Singular Value Decomposition
J. Phys. Soc. Jpn. 91, 114001 (2022) 
https://doi.org/10.7566/JPSJ.91.114001

機械学習の理論的研究は昔から調べられていて、さまざまなアプローチがある。統計力学という物理学のアプローチも昔からある。例えば、H. Sompolinsky, N. Tishby, and H. S. Seung, Physical Review Letters  65, 1683 (1993)などである。もっと前からあるかもしれないし、E.Gardnerを挙げるべきかもしれない。いずれにしても、この方向性は、特定の重みをもった機械学習器の性能を調べるのではなくて、典型的な性能を調べることである。

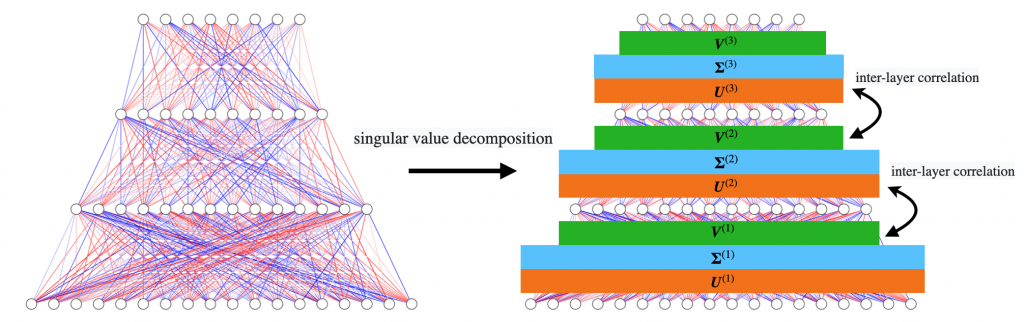
市川くんのこの論文もその方向性であり、ランダム系の統計力学の手法であるレプリカ法を用いた深層ボルツマンマシンの典型的な性能に関する研究である。ボルツマンマシンは、一般に模したいデータ集合を訓練データとして、その生成確率を真似する生成器である。結果として、学習がうまくいけばデータを模したデータを生成することができる。ここで、何に関する典型的な性能なのかには少し自由度があって、特定のデータではなく、いろんなデータに対する典型的な性質であることもあるし、いろんなデータを学習した結果として得られるいろんな重みに関する典型的な性質であることもあるだろう。市川くんの研究では後者に属するのだけど、ちょっと工夫をしていて、重みの確率分布を与えるのではなくて、重みを特異値分解して、その特異ベクトルに確率分布を導入したことにある。学習後の重みを特異値分解すると、ごちゃごちゃしたランダムに見える特異値たちがランダム行列っぽく見えて、学習の結果として現れる特異値はそのランダムな特異値分布から数個飛び出している。この性質を取り込んだ深層ボルツマンマシンの研究である。

この設定で、大自由度極限のもとで相図を描いてみた。理論的には、その特異ベクトルの成分に関する平均を明示的に取らずに最後の方まで行けるので、その分布がガウス分布なのか、もっと他の分布なのかは何でもよい。相境界の安定性解析をするときに、相によって何次のモーメントが関わってくるかが変わってくる。シンプルな学習成功相は二次モーメントで決まるので、分布の詳細によらないことになる。ちょっと面白い。深層型にしたので、そこに相間の相関を導入することができて、それが学習成功相のより重要な性質を決めるために本質的な役割をしていることも明らかになった。学習段階で、どのように相関を獲得するかはこの研究ではわからない。

ただ、実際の学習データを使った計算でも、相関は出ていて、この研究であきらかになった相構造を反映していることがわかっている。学会発表では見せたが、うーん、そこはまだ論文にしていないのでここでは書けない。。。あーなるほど、そういうことが起きているのねって感じです。